

Explored by:
Aubrey D. Johnson
In this assignment we will construct a basic triangle and then construct multiple orthocenters within the main triangle. Remember, an orthocenter is the common intersection of the thee altitudes of a triangle or their extensions (according to Webster.com).
So will start with a basic triangle.

Now we will construct the altitudes for this triangle. An altitude of a triangle is a strait line through a vertex and perpendicular to the opposite side or an extension of the opposite side (according to Wikipedia).
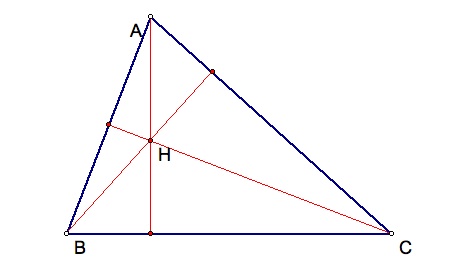
Now we see the Orthocenter for triangle ABC. I will show you a picture of the original triangle with triangle HBC highlighted so we all know what we are discussing.

Now we will construct the orthocenter of triangle HBC. We will still use the previous definition of an orthocenter from Wikipedia.
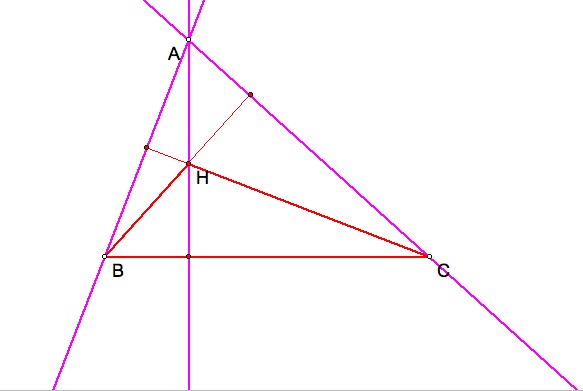
This is very interesting. Notice that the Orthocenter for triangle HBC is angle BAC of the original triangle. If you recall the definition of the orthocenter, the orthocenter is the perpendicular line (90 degree angle) of the line segment of a vertex and its opposite side, OR the extension of that side. For triangle HBC the orthocenter is created by the extension of segments BH and CH. Now we will clean up the triangle and redefine the original triangle in blue with segments BH and HC in highlighted red. To emphasize the dual importance of point A, we will highlight A in pink.
I now want to identify the orthocenter for triangle HAC. I will highlight triangle HAC in purple and then construct the orthocenter for HAC.
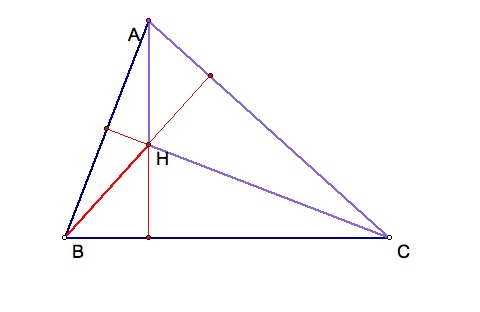
Now that we know which triangle we will be working with, we will find the orthocenter of HAC.
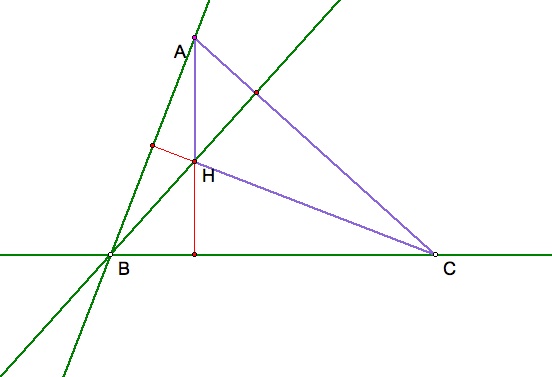
Recall the definition, and notice that triangle HAC's orthocenter is angle ABC. We will now identify triangle HAB. Point B will now be highlighted green to display its dual importance.

We will now construct the orthocenter of HAB.
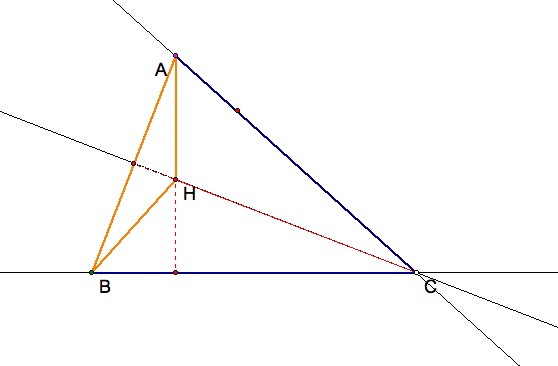
Notice that HAB's orthocenter is angle BCA. We will now highlight point C gold to display its dual importance.
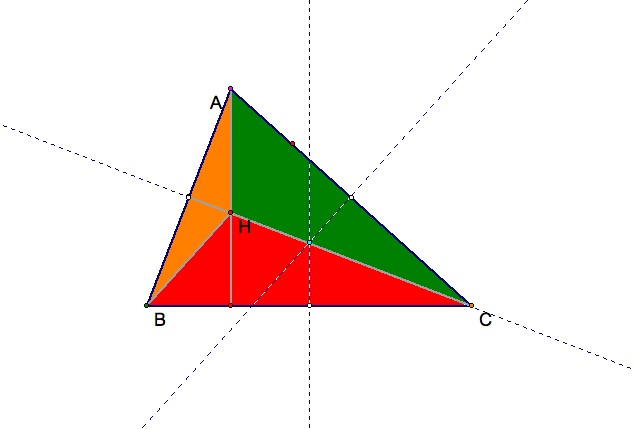
Moving on with our investigation well will color the interior of triangle HAB gold, HAC green and HBC red leaving the points their designated colors.
We will now construct circumcircles using our new triangle. Recall, a circumcircle is a circle that passes through all the vertices of a triangle (according to Webster.com).
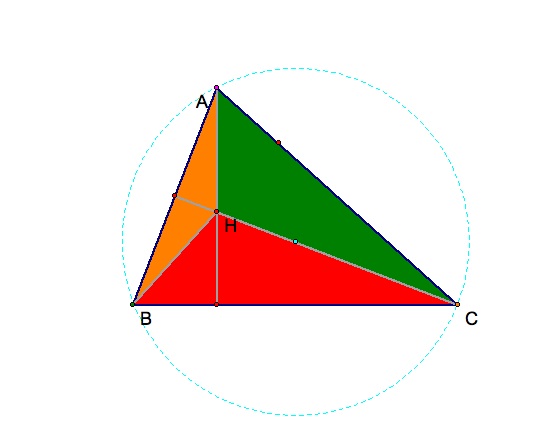
First we will construct the circumcircle for the overall triangle, ABC. First we must find the circumcenter of ABC, it has been highlighted in cyan.
The Circumcirlce will be in dashed cyan and the the dashed black lines will disappear.
Now I will construct the circumcenters and circumcircles for HBC (red dashed), HAB (gold dashed) and HAC (green dashed).
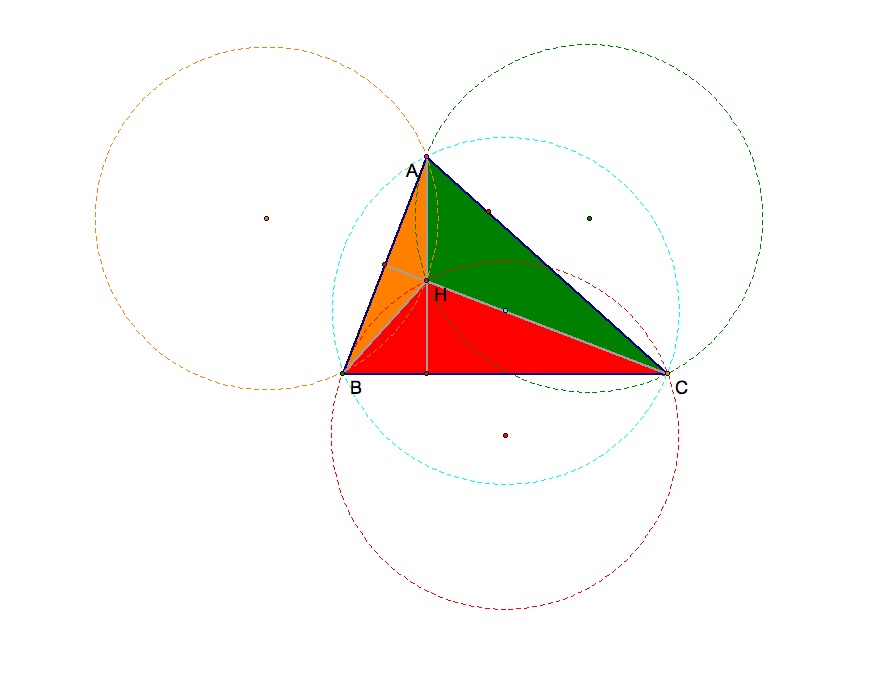
Now I will connect all of the circumcenters with a black line. Then I will connect all the vertices of the main triangle to the circumcenter of the larger triangle. Notice the shape that is formed.

The black lines appear to create a rectangular prism with a square base. We were able to create this shape from a simple triangle.
Lets move angle BAC to the orthocenter, H, and see what happens to the other figures in our picture....

Notice how everything has disappeared and we are only left with a smaller version of the basic triangle with the altitude from BC to BAC the only extra drawing present. to see the motion click: Moving Triangle